Ausgangslage (wer nicht alles lesen will, verwendet einfach die rote Formel für die 10/10-Gebühr!)

In 0022.htm wird die sehr stark verkürzte Darstellung von zusammengesetzten, zunehmend steigenden oder fallenden, linearen Funktionen gezeigt durch Reihung der Parameter m (D) und n (K, L) in Arrays. Wie aber geht man vor, wenn eine solche Funktion dem Grunde nach linear ist, jedoch zwischen den Abschnitten unterschiedlich hohe (F) und unterschiedlich breite (D) Stufen in der Funktion vorliegen, wie bei deutschen Notargebühren? (Die Großbuchstaben greifen schon vor auf die gleich folgende Gebührentabelle.)

Die Notargebühren, hier als 10/10, sind wie folgt vorgegeben (die +2 bei der Gebühr ergeben sich aus der Mindestgebühr von 10 Euro), Grundlage: KostO §§18 I und 32, inhaltlich angeregt durch http://www.excelformeln.de/formeln.html?welcher=435:

 A            B          C       D   E   F     G H           I J            K L  MNO P  Q  R
1 Wert      von        bis      je mal mit Summe %   +2=Gebühr kum=eff%|n=f(0)K0    K1 K2 K3
2          0,01      5.000   1.000   5   8    40 0,8        42 0,84    |   10 0    515 15  9
3      5.000,01     50.000   3.000  15   6    90 0,18      132 0,264   |   42 0,2  545 15  3
4     50.000,01  5.000.000  10.000 450  15  7425 0,1485   7557 0,15114 |   72 0    610 10  6
5  5.000.000,01 25.000.000  25.000 800  16 12800 0,0512  20357 0,081428| 4373 0    705  5  3 
6 25.000.000,01 50.000.000  50.000 500  11  5500 0,011   25857 0,051714|14868 0  50050 50  1
7 50.000.000,01 60.000.000 250.000  40   7   280 0,0005  26137 0,043562|24464 0  ===========
8 60.000.000,01 Gebührenmaximum erreicht   

Lösung (siehe unten auch die Grafik zur Veranschaulichung)

Alternative 1: C1:
=MIN(KÜRZEN(((A1-1%)%%-{0;0,2;0;0;0;0})/{0,1;0,3;1;2,5;5;25})*{8;6;15;16;11;7}+{10;42;72;4373;14868;24464};26137) +SUMMENPRODUKT((ABS(A1%-{515;545;610;705;50050}-50%%%)<{15;15;10;5;50})*{9;3;6;3;1}) 
Achtung: SpreadCE benötigt dies als Matrixformel - SUMME statt SUMMENPRODUKT reicht dort dann aus.

Alternative 1 kürzer mit Zellverweisen statt harter Arrays als Matrixformel:
{=MIN(KÜRZEN(((A1-1%)%%-L)/D%%)*F+K;26137)+SUMME((ABS(A1%-P-50%%%)<Q)*R)}
(als normale Formel geht es nicht, da MIN zwar harte Arrays, aber keine benannten Bereiche ohne "Extra-Kick" verarbeitet), 
wenn D2:D7 als D usw. und P2:P6 als P usw. benannt ist, siehe dazu auch Quizfrage 2!

oder

Alternative 2: B1: Einfügen Namen Definieren "Notargebuehr" bezieht sich auf
=AUSWERTEN("=MIN(KÜRZEN((("&!A1&"-1%)%%"&WAHL(VERGLEICH((!A1-1%)%%;{0;0,5;5;500;2500;5000})
;")/,1)*8+10";"-,2)/,3)*6+42";"))*15+72";")/2,5)*16+4373";")/5)*11+14868";")/25)*7+24464")&";26137)")+JETZT()*0

Alternative 2 kürzer: B1: Einfügen Namen Definieren "Notargebuehr" bezieht sich auf
=AUSWERTEN("=MIN(KÜRZEN((("&!A1&"-1%)%%"&SVERWEIS((!A1-1%)%%;O;2)&";26137)")+JETZT()*0
wenn M2:N7 als O benannt ist:

     M    N
1 Grenzen Funktions-Ende  
2    0    )/,1)*8+10
3    0,5  -,2)/,3)*6+42
4    5    ))*15+72
5  500    )/2,5)*16+4373
6 2500    )/5)*11+14868
7 5000    )/25)*7+24464

Bei Alternative 2 am Ende nicht vergessen: B1: =Notargebuehr. 

Alle 4 Versionen abschließend unter Excel 2000 getestet! 

Erläuterung

Die beiden Alternativen sind gleich lang und benötigen beide A1 zweimal als Variable. Alternative 1 läuft auch auf Systemen ohne benannte Formeln.

Die Lage und Größe der Stufen werden durch 4 Parameter bestimmt:
- X-Achsen-Korrektur zum Y-Achsen-Schnittpunkt (bei X=0): hier -{0;0,2;0;0;0;0}
  Nötig, falls gleiche Stufenbreiten eines Funktionsabschnitts nicht bei 0, sondern davon verschoben begännen
- fiktiver Y-Achsen-Schnittpunkt: hier +{10;42;72;4373;14868;24464}
- Stufenhöhe: hier *{8;6;15;16;11;7}
- Stufenbreite: hier  /{0,1;0,3;1;2,5;5;25}
Sie werden bei Alternative 2 direkt als 6 einzelne Formeln geschrieben und somit anders sortiert.

Alternative 2 ist eine benannte Formel, die mittels der Excel4-Makrofunktion =AUSWERTEN() kürzer gehalten werden kann als etwa eine Reihung von 4 SVERWEIS()-Funktionen, die jeweils die Daten {0;0,5;5;500;2500;5000} neu enthalten müssten. SpreadCE kann nicht mit allen benannten Formeln, die in Excel möglich sind, umgehen, z.B. AUSWERTEN(). In anderen Worten (vermutet, aber unbewiesen): Tabellenfunktionen ja, Excel4-Makrofunktionen nein.

Alternative 1 befolgt zunächst 0022.htm, ergänzt um die 2 zusätzlichen Parameter für die Stufen zu denen für Steigung und Lage. Dann muss aber mit dem SUMMENPRODUKT()-Term an einzelne Funktionsabschnitte Hand angelegt werden, siehe hier:

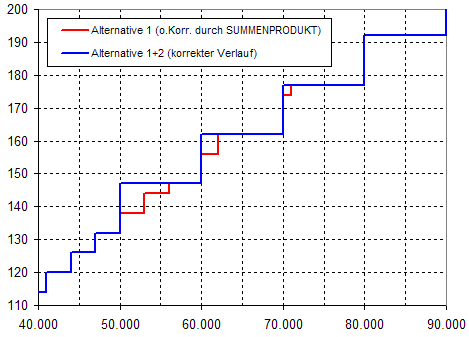
Beispiel: Ab über 50.000 Euro bezahlt man für jede angefangenen 10.000 Euro 15 Euro zusätzliche Gebühr; davor waren es für jede angefangenen 3.000 Euro nur 6 Euro. Begnügte man sich mit dem MIN()-Term, gälten bis 71.000 Euro wechselseitig beide Abschnitte und damit zwischenzeitlich falsche (rote) Ergebnisse! Für 50.000,01 ergäbe der unkorrigierte Term bspw. 138 statt richtig 147, daher die Korrektur um 9 mittels {9;3;6;3;1}. Die letzte Korrektur (um 1) ist hier nicht zu sehen, da sie erst zwischen 5.000.000 und 5.010.000 anfällt. Das brächte die Grafik aus dem gewollten engen Ausschnitt, wodurch der Sachverhalt optisch nicht mehr deutlich darstellbar wäre. Excel-Datei für diese Grafik: Hier. Siehe auch Quizfrage 1

Anders ausgedrückt: Die unteren rechten Ecken der roten Linie fahren mit der höheren Steigung der Gebühr fort, wie es bis 50.000 Euro der Fall war. Durch die größeren Stufen über 50.000 Euro ist ihre fiktive Fortsetzung trotz größerer Steigung deshalb minimal, da die Stufenhöhen geringer sind.

Quizfrage 1: Wann wird der SUMMENPRODUKT()-Term nicht gebraucht? Antwort: Bei monoton fallendem F (Bereich F2:F7).

Quizfrage 2: Was ist der Unterschied zwischen B:N und P:R? Antwort: A:L beschreibt die 6 linearen Funktionen, P:R die 5 zu reparierenden Bereiche aufgrund nicht monoton fallendem F, siehe Quizfrage 1.